데이터 탐색 과정
| 구분 | 묘사적 데이터 분석 (DDA: Descriptive Data Analysis) |
탐색적 데이터 분석 (EDA: Exploratory Data Analysis) |
확증적 데이터 분석 (CDA: Confirmatory Data Analysis) |
예측적 데이터 분석 (PDA: Predictive Data Analysis) |
| 목적 | 현재의 모습을 요약하여 기술 수집된 데이터의 표현 | 수집된 데이터를 탐색하여 이해하고, 가설 도출 | 도출된 가설 검정 | 관계식을 만들고 최적의 조건을 예측 |
| 분석도구 | 평균, 표준편차, 빈도수, 백분위수, 첨도, 왜도 등 | 그래프 분석(히스토그램, 파레토 파트, Box Plot 등) 정규성 확인, 트렌드 분석 |
추정(점추정, 구간추정) 가설검정(Z검정, t검정, 분산분석, 회귀분석 등) |
모델링 기법(K-NN, Nueral Network, 선형회귀 등), 시뮬레이션 기법 등 |
탐색적 데이터 분석과 확증적 데이터 분석의 비교
| 구분 | 탐색적 데이터 분석(EDA) | 확증적 데이터 분석(CDA) |
| 목적 | 새로운 가설 생성 및 통찰을 얻어 방향성 설정 | 가설 검정의 유효성 검정 행동에 대한 평가로 채택 여부 결정 |
| 절차 | 유연한 절차 데이터 수집 → 시각화 탐색 → 패턴 도출 → 인사이트 발견 |
엄격한 절차 가설설정 → 데이터 수집 → 통계분석 → 가설검정 |
| 장점 | 분석 과정에서 유연하게 가설을 설정 가능 | 검증된 이론과 모형이 존재 |
| 단점 | 명확한 분석 목표가 없으면 분석의 오류를 범할 수 있음 | 선입견이 개입되어 예상치 못한 결과이 사전 탐지가 어려울 수 있음 |
| 사용 통계 | 기술통계: 평균, 퍼센트, 분포 등 요약 정보, 그래프에 의한 시각화 자료 | 추론 통계: 검정통계량 및 모수 기준치와의 차이(추정, 가설검정) |
| 사례 | 지역별/시기별 배달음식 주문 데이터를 탐색하고 시각화하면 매출이 높을 것으로 예측되는 장소와 주문이 많은 시간에 대한 정보를 얻을 수 있음. | CCTV의 범죄 예방 효과를 검증하기 위해 CCTV설치 수와 범죄 발생빈도의 통계적 상관관계를 파악하여 CCTV가 설치된 곳은 범죄 발생빈도수가 높다 혹은 낮다 등의 가설을 검증하는 방법으로 확증적 데이터 분석 설명할 수 있음 |
탐색적 데이터 분석의 4가지 주제
| 구분 | 설명 | 예시 |
| 저항성 | 데이터의 일부가 파손되었을 때, 영향을 적게 받는 성질 자료가 파손된다는 것은 일부가 예상치 못한 값으로 대체되는 경우를 의미하며, 저항성이 존재하면 예상치 못한 값에 의한 변화에 민감하지 않게 됨 |
평균보다 중앙값이 이상값에 덜 민감함 |
| 잔차의 해석 | 예측값의 잔차를 계산하여 특정 데이터가 보통 데이터와 다른 경향을 가지고 있는지 확인 잔차(Residual): 관측값들이 주경향으로부터 얼마나 벗어나는지를 알 수 있는 척도 |
잔차를 산출했을 때, 다른 데이터(관측값)와는 달리 왜 큰 잔차가 발생했는지 확인이 필요함 |
| 데이터의 재표현 | 재표현: 데이터의 해석과 분석을 단순화하기 위해 원 변수를 재표현하는 방법 일반적으로 데이터를 재표현하여, 분포의 대칭성, 선형성, 분산 안정성 등 데이터 구조 파악 |
Swewed Right 데이터 분포 같은 경우 평균과 중앙값이 달라져 어떤 값을 대표값으로 사용해야 하는지 혼란 야기 |
| 데이터의 현시성 | 현시성: 데이터를 그래프로 시각화함으로써 데이터 안에 숨겨진 정보를 효율적으로 파악하는 과정 시각화는 낮은 수준의 분석이지만 EDA에서 필수이며, 수치 기반의 복잡한 분석보다 직관적으로 통찰력을 얻을 수 있음 |
히스토그램을 통해 구간의 빈도수가 많은 곳을 시각적으로 알 수 있음 |
상관관계 분석의 이해
- 상관관계를 파악하여 분석을 위한 독립변수와 설명변수 등을 파악
- 이상값 제거, 패턴 발견
상관관계 분석의 정의
- 선형적 과계 분석, 선형성 강도에 대한 통계적 분석
상관관계 분석의 가정사항
| 가정사항 | 설명 |
| 이변량 | 비교 가능한 두 개의 연속형 변수 존재 |
| 정규분포 | 변수 중 적어도 하나의 변수가 정규분포를 만족하는지 여부 (정규성을 만족) |
| 선형성 검증 | 연속형 두 변수 간에는 선형적인 관계 존재 상관관계 분석 전에 두 변수 간의 산점도를 그려 선형성이 있는지 확인해야 함 |
상관관계 해석
| 구분 | 설명 |
| 선형성 | 두 개의 변수 간의 직선관계(비례식) |
| 선형관계의 방향 (단조성) |
양(+)의 상관관계: 한 변수의 값이 증가함에 따라 다른 변수값도 증가 음(-)의 상관관계: 한 변수의 값이 증가함에 따라 다른 변수값은 감소 0: 선형 상관관계 없음 |
| 관계의 크기(강도) | - 1 ~ +1 사이의 값 -1, +1: 완전한 선형관계  피어슨 상관계수의 크기 |
공분산의 정의

- 공분산(Covariance)은 두 변수 X, Y가 서로 어떤 패턴(Pattern)을 보여주는가를 나타내는 지표
- 두 변수는 질적변수가 아닌, 크기가 측정되는 양적 변수
공분산의 해석

- 공분산 값이 0보다 크면 양(+)의 관계, 0보다 작으면 음(-)의 관계, 0인 경우는 서로 상관이 없음(독립의 의미X)
공분산 분석 사례
| 구분 | 설명 |
| 사례 | A중학교에 다니는 학생 5명의 영어, 국어 점수의 연관성 확인 사례 <영어점수, 국어점수>  |
| 설명 |  |
| 설명 | 주어진 표본의 영어점수, 국어점수의 평균은 5이다. 각 학생의 점수에서 평균을 뺸 편차를 구한다. 영어와 국어 편차의 곱의 합은 17. 여기에 5명의 표본으로 연관성을 분석하고 있기 떄문에 표본공분산을 적용하여 4(n-1, 자유도)로 나누어 주었다. 공분산은 4.25가 도출된다. |
| 분석 | 국어평균과 영어평균의 산점도를 확인하면 각 평균 5로부터 5명의 학생의 점수 분포를 확인할 수 있고 공분산은 0보다 큰 4.25가 산출되었기 떄문에 영어점수가 증가할 때 국어점수도 증가하는 것으로 확인된다. |
상관계수 종류
- 상관계수(Coreelation Coefficient): 공분산을 각 변수의 표준편차로 나눈 것(표준화)
- 피어슨 상관계수: 특정 분포를 따르면서(모수적) 등간척도 및 비율척도와 같은 연속형의 데이터에 적용
- 스피어만 상관계수, 켄달 상관계수: 특정 분포를 가정하지 않으면서(비모수적) 서열척도 변수인 경우 주로 이용
+모수적방법, 비모수적방법
- 모수 방법(Parametric method): 모수를 특정 분포로 가정하여 접근하는 방법
- 비모수적 방법(Non-Parametric method): 모집단의 특정 분포를 가정하지 않고 접근하는 방법
상관계수의 선택 기준 비교
| 구분 | 피어슨 | 스피어만 | 켄달 |
| 변수 유형 | 등간/비율변수 - 등간/비율변수 | 서열변수 - 서열변수 | 서열변수 - 서열변수 |
| 목적 | 등간변수, 비율변수들의 상관관계 측정 | 서열변수들의 상관관계 측정 | 서열변수들의 상관관계 측정 |
| 정규성 | 정규성 가정(모수적 방법) | 정규성 가정(비모수적 방법) | 정규성 가정 안함(비모수적 방법) |
| 관계 | 선형관계 | 비선형관계, 단조성(X증가 → Y증가) | 비성형관계, 단조성(X증가 → Y증가) |
| 상관계수 | γ, 감마(적률 상관계수) | ρ, 로우(순위 상관계수) | τ, 타우(켄달) |
| 범위 | -1 ≤ γ ≤ 1 | -1 ≤ ρ ≤ 1 | -1 ≤ τ ≤ 1 |
+편상관계수(Partial Correlation Coefficient)
- 부분상관계수로도 부르며, 제3변수의 영향을 고려하지 않는 상관계수와 달리 제 3변수 고려
- 3변수가 주은 요인 p-1개를 제어하고 두 변수의 순수한 상관관계를 나타낸다.
- 예) 학습시간과 시험점수 간의 상관관계에서 나이의 영향 제외
피어슨 상관계수(PCC: Pearson Correlation Coefficient)
피어슨 상관계수의 정의

피어슨 상관계수 방향성 및 크기(강도)
| 범위 | 설명 |
| 선형관계의 방향 | 양(+)의 상관관계: 한 변수의 값이 증가함에 따라 다른 변수값도 증가 음(-)의 상관관계: 한 변수의 값이 증가함에 따라 다른 변수값은 감소 0: 선형 상관관계 없음 |
| 관계의 크기(강도) | -1, +1: 완전한 선형관계(강한 상관관계) ±0.3 미만이면 약한 선형 상관관계 ±0.7 이상이면 강한 성형 상관관계 |
스피어만 상관계수(SROCC: Spearman Rank-Order Correlation Coefficient)
스피어만 상관계수의 정의
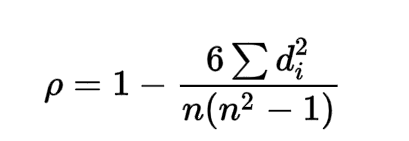
di = xi의 순위 - yi의 순위, n: 상수
- 피어슨 상관계수: 수학점수와 영어점수의 상관계수
- 스피어만 상관계수: 수학과목의 석차와 영어과목의 석차
- 스피어만 상관계수(로우)는 데이터 내 편차와 에러에 민감하며, 일반적으로 켄달 상관계쑤보다 높은 값
+ 선형관계와 단조관계
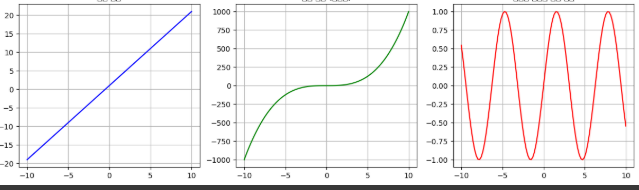
선형관계, 단조관계(비선형), 선형도 단조도 아닌 관계
단조성이 좋다: 한 변수의 값의 크기가 커지면(또는 작아지면) 다른 변수의 크기도 커진다(또는 작아진다)는 의미
켄달 상관계수
켄달상관계수의 정의
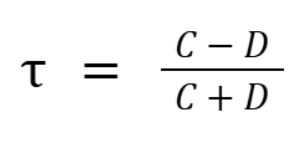
C(Concordant Pair): 부합하는 쌍의 수
D(Discordant Pair): 부합하지 않는 쌍의 수
- X의 순위와 일치시키기 위해 Y를 얼마나 바꾸어야 하는 정도로 상관관계 평가
- xi가 커질 떄 yi도 커지면 부합, xi가 커질 떄 yi가 작아지면 비부합
- 켄달 상관계수(타우)는 샘플 사이즈가 작거나 데이터의 동률이 많을 때 유용하다.
상관계수의 유의성 검정
- '통계 기법 이해'를 학습한 뒤 다시 학습하는 것을 추천! -> 대학에서 확통 강의 들었다면 평범한 내용
- 통계적으로 유의하다 = 관찰된 현상이 우연에 의해 벌어졌을 가능성이 낮다
- 상관계수 유의성 검정: 모수관계수인 p를 사용하여 가설 설정하고 검정
- 통계적 유의성 검정: 귀무가설(상관계수가 0), 대립가설(상관계수가 0이 아니다) 양측검정
- p값(P-Value)이 0.05보다 작다면, 통계적으로 유의미한 상관계수
피어슨 상관관계 분석 사례
| 구분 | 설명 |
| 사례 | A중학교에서 학생들의 지각횟수와 국어성적의 상관관계를 확인하기 위해 5명의 학생을 무작위로 표본으로 선정하여 분석하였다. |
| 피어슨 상관계수 정의 |  |
| 풀이 | 지각횟수 평균: 3 국어성적 평균: 6  = -0.9 |
| 분석 | 피어슨 상관계수는 -1에 가까우므로 지각횟수와 국어성적은 음의 상관관계가 높음 |
상관계수 유의성 검정 절차
| 절차 | 설명 |
| 귀무가설 및 대립가설 설정 | 귀무가설(H0): p = 0 (상관관계가 0이다, 상관관계가 없다) 대립가설(H1): p ≠ 0 (상관관계가 1이다, 상관관계가 있다) |
| 유의수준(α) 결정 | 0.05, 0.1 등을 사용 |
| 기각역 설정 | 양측검정: 대립가설 H1: p ≠ 0일 때, |
| 검정통계량 계산 |  |
| 통계적 결론 | 검정통계량이 기각역에 속하면 귀무가설 기각, 아닌 경우 귀무가설을 기각하지 않음 |
상관계수의 유의성 검정 사례
| 구분 | 사례 |
| 사례 | A중학교에서 학생들의 지각횟수와 국어성적의 상관관계를 확인하기 위해 5명의 학생을 무작위로 표본으로 선정하여 분석하였다. 상관계수는 -0.9일 때 유의수준 10%에서 상관관계가 있다고 할 수 있는지 검정해보자. |
| 귀무가설 및 대립가설 설정 | 귀무가설(H0): p = 0 지각횟수와 국어성적은 상관관계가 없다. 대립가설(H1): p ≠ 0 지각횟수와 국어성적은 상관관계가 있다. |
| 유의수준 | α = 0.1 |
| 기각역 및 기각값 | - 유의수준 0.1에대하여, 양측검정이므로 𝛼/2 = 0.05이고 자유도는 3(5-2)인 값을 T분포표에서 확인하면 ±2.354이다. |
| 검정통계량 및 P값 |  |
| 분포도 |  |
| 통계적 결론 - 기각역 | 검정통계량 t = -3.58은 기각역에 속하여 귀무가설은 기각된다. 따라서 지각횟수와 국어성적은 상관관계가 있다. |
| 통계적 결론 - p값 사용 | p(0.037) < 유의수준( α = 0.1), P값이 유의수준보다 작으므로 귀무가설은 기각된다. 따라서 지각횟수와 국어성적은 상관관계가 있다. |
기초통계량의 이해
- 중심경향치(분포의 중심): 평균(Mean), 중앙값(Median), 최빈값(Mode)
- 산포도(분포의 흩어짐): 표준편차(Stddev), 분산(Variance), 범위(Range), 사분위수(Quartile), 변동계수(CV)
- 비대칭도(분포의 모양): 왜도(Skewness), 첨도(Kurtosis)
중심경향치(Central Tendency)
- 자료 전체를 대표할 수 있는 값을 의미
- 평균, 최빈값, 중앙값 등
평균(Mean)
산술평균(Arithmetic Average)
- 산술평균 = 관측된 숫자들의 총합 / 관측된 숫자들의 총 개수
모평균과 표본평균
| 모집단의 평균(모평균) | 표본집단의 평균(표본평균) |
 |
 |
| N: 모집단의 자료에서 관측값의 총 개수 n: 표본집단의 자료에서 관측값의 총 개수 μ: 모집단평균 x̅: 표본 평균(X바) xi: 자료의 i번째 관측값 |
자료 1,4,6,5,6,2의 평균은 (1+4+6+5+6+2)/6=4인데, 극단치 100이 존재한다고 가정했을 때 평균은 (1+4+6+5+6+2+100)/7=19.2이 된다. 일반적인 값을 넘어서는 극단치가 데이터의 일반화를 훼손시킬 수 있다. |
절사평균(Trimmed Mean)
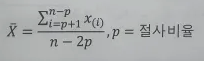
- 극단치가 존재할 경우 극단값을 제거하는 효과
가중평균(Weighted Mean)

- 각 데이터 값에 가중치를 곱한 값들의 총합을 다시 가중치의 총합으로 나눈 값
가중평균 예시
- A학생과 B학생의 영어점수와 수학점수는 각각 다음과 같다.
| 이름 | 영어 점수 | 수학 점수 | 산술평균 |
| A학생 | 50 | 70 | 60 |
| B학생 | 60 | 60 | 60 |
- 산술평균은 A학생 = B학생
- 영어의 가중치를 50%, 수학의 가중치를 70%라 했을 때 가중평균은 다음과 같다. (정시 입시같은 것..)
| 이름 | 영어 점수 | 영어 가중치 | 수학 점수 | 수학 가중치 | 가중평균 |
| A학생 | 50 | 50% | 70 | 70% | (50 * 0.5 + 70 * 0.7) / (0.5 + 0.7) = 61.67 |
| B학생 | 60 | 50% | 60 | 70% | (60 * 0.5 + 60 * 0.7) / (0.5 + 0.7) = 60 |
기하평균(Geometric Mean)
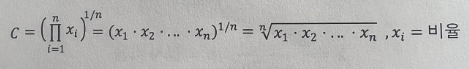
- n개의 양수 값을 모두 곱한 값에 n제곱근을 적용한 값
- 변수가 성장률(물가 상승률, 연평균 성장률 등) 또는 변화율(인구변동률 등)일 때 유용한 중심위치 척도
- 예시
- A마우스의 출시 가격이 10,000원이었는데, 2월에 20% 가격이 증가하고, 3월에 30%의 가격이 증가하였으며, 4월에는 10% 감소하였다. 3개월 평균 증가율은 다음과 같다.
| 출시 가격 | 2월 가격 | 3월 가격 | 4월 가격 |
| 10,000 | 12,000 | 15,600 | 14,040 |
| 출시 가격 | 2월 변화율 | 3월 변화율 | 4월 변화율 |
| 1 | 1.2 | 1.3 | 0.9 |
- (1.2 * 1.3 * 0.9)^(1/3) = 1.12
- 기하평균 약 1.12로 3개월동안 평균 약 12% 가격이 증가했다.
산술평균은 (20 + 30 - 10) = 13.13% 가격이 증가한 것으로 산출
조화평균(Harmonic Mean)
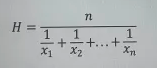
- 역수의 산술평균의 역수를 구한 값
- 역수의 차원에서 평균을 구하고, 다시 역수를 취해 원래 차원의 값으로 돌아오는 것
- 평균적인 변화율을 구할 떄 주로 사용하며, 속도 등과 같이 여러 단위가 결합되어 있을 때 활용 가능
- 조화평균 예시

중앙값(Median = 중위수 = 중앙치)
- 중심에 위치한 값
- n=홀수: (n+1)/2의 값
- n=짝수: (n/2의 값 + (n/2+1)의 값)/2
중앙값 예시
| 구분 | 전체 자료의 개수(n)가 홀수인 경우 | 전체 자료의 개수가 짝수인 경우 |
| 정렬값 | 1, 2, 4, 8, 15 | 1, 2, 4, 5, 7, 10 |
| 중앙값 위치 | (5+1) / 2 = 3 | (6/2 + 1) = 4 |
| 중앙값 | 3번째 값 = 4 | (3번째 값 + 4번째 값) / 2 = (4 + 5) / 2 = 4.5 |
최빈값(Mode)
- 빈도수가 가장 많은 값, 극단치에 영향 X, 같은 값이 많이 반복될 때 유용
- 모든 자료의 수가 1번씩 나올 경우 최빈값 존재X, 여러개의 최빈값이 있을 수 있다.
평균, 중앙값, 최빈값의 비교
- 극단치가 존재하는 경우 평균보다 중앙값이 더 합리적이지만
- 평균에 대한 수학적 전개가 용이하고 평균의 분포 함수를 쉽게 구할 수 있기 때문에
산포도
- 데이터가 흩어져 있는 정도, 중심위치가 얼마나 안정적인지에 대한 정보
- 범위, 사분위수 범위, 분산, 표준편차, 변동계수 등
범위(Range)
- Range = Max - Min
사분위수 범위(IQR: Interquartile Range)
- IQR = Q3 - Q1
편차(Deviation), 분산(Variance)과 표준편차(Standard Deviation)

편차, 분산, 표준편차 차이
| 편차 | 분산 | 표준편차 |
| 각 관측치와 평균의 차이 | 편차의 제곱합의 평균 | 분산의 제곱근 |
+ 표본을 n-1로 나누는 이유
- 자유도(Degree of Freedom)에 관한 문제
- 자유도: 자료로부터 통계량을 계산하는 경우 이 통계량에 대해 독립적인 정보를 갖는 자료 측청치의 개수
표준편차 분석 예시
| 구분 | 설명 |
| 사례 | A학교의 3학년 1반의 수학점수{20, 30, 40, 60, 100}와 3학년 2반의 수학점수{40, 45, 50, 55, 160}는 동일하게 평균이 50점인데, 어느 반의 학습성과가 높다고 할 수 있을까? |
| 표준편차 | 3학년 1반 표준편차: 31.9 3학년 2반 표준편차: 7.9 |
| 산포도 | 3학년 2반이 평균을 중심으로 성적이 가깝게 형성되어 산포도가 낮음을 의미한다. 따라서 3학년 2반이 수학성적이 골고루 분산되어 있어, 학업성취도가 높다고 분석할 수 있다. |
표준편차(Standard Deviation)와 표준오차(Strandard Error)
- 표준오차는 표본을 여러 번 추출했을 떄, 여러번 추출한 표본들의 평균의 표준편차
- 각 표본의 평균이 얼마나 변동하는지 측정하는 것
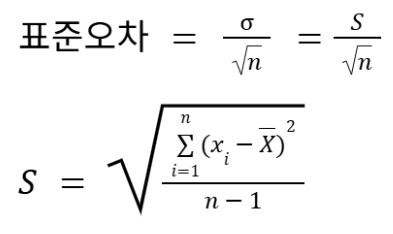
변동계수(Coefficient of Variation)
- 표준편차 / 평균 * 100
변동계수 분석 예시
| 구분 | 설명 |
| 사례 | A고등학교 1학년인 홍길동, 성춘향 학생의 공부습관을 한 달간 조사하여 홍길동 학생은 평균 8시간, 표준편차는 0.5의 학습성향을 파악했고, 성춘향 학생은 평균 6시간, 표준편차 0.8인 학습결과를 얻었다. 어느 학생이 더 꾸준히 공부하는 습관을 가졌을까? |
'변동계수 |
홍길동의 학습 변동계수 = 0.5/8 * 100 = 6.3 성춘향의 학습 변동계수 = 0.8/6 * 100 = 13.3 |
| 분석 결과 | 변동계수 계산 결과, 홍길동(6.3)이 성춘향(13.3)보다 차이가 작다는 걸 알 수 있다. 따라서 홍길동 학생이 더 꾸준히 공부하는 습관을 가지고 있다고 결론을 얻을 수 있다. |
비대칭도
-
-
왜도(Skewness)
-
왜도의 분포도
| 왜도 < 0 | 왜도 = 0 | 왜도 > 0 |
 |
 |
 |
| Left Skewed (Negative Skewness) 왼쪽으로 긴 꼬리를 갖는 분포 |
좌우대칭 분포 | Right Skewed (Positive Skewedness) 오른쪽으로 긴 꼬리를 갖는 분포 |
| 평균< 중앙값 < 최빈값 | 평균 = 중앙값 = 최빈값 | 최빈값 < 중앙값 < 평균 |
첨도(Kurtosis)
-
-
첨도의 분포도
| 첨도 < 0 | 첨도 = 0 | 첨도 > 0 |
 |
 |
 |
| 퍼짐분포(Platykurtic) | 정규분포(Mesokurtic) | 폭이 좁은 분포(Leptokurtic) |
| 정규분포보다 짧은 꼬리를 갖음 완만한 모양 |
좌우대칭 분포 표준정규분포와 뾰족한 정도가 유사 |
정규분포보다 긴 꼬리를 갖음 뾰족한 모양 |
시각적 데이터 탐색의 이해
정보 시각화 방법
| 시간시각화 | 분포시각화 | 관계시각화 | 비교시각화 | 공간시각화 |
| 막대그래프 누적 막대그래프 점그래프 선그래프 영역차트 계단식그래프 |
파이차트 도넛형차트 트리맵 누적연속그래프 줄기잎그림 상자그림 히스토그램 |
산점도 산점도행렬 버블차트 히스토그램 |
플로팅바차트 히트맵, 모자이크 그림 체르노프페이스 스타차트 평행좌표그래프 다차원척도법 |
등치지역도 등치선도 도트맵 버블플로트맵 카토그램 |
시간시각화 탐색
막대그래프
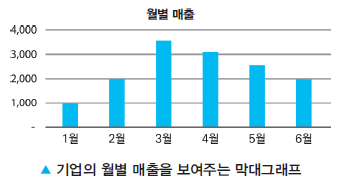
- 바차트(Bar Chart): 막대가 가로로
- 컬럼차트(Column Chart): 막대가 세로로
누적막대그래프
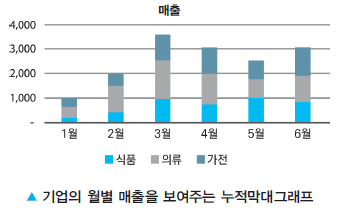
- 변수 여러개를 동시에 다루는 경우 세부항목 각각의 값과 전체의 합을 함께 표현하기 용이
점그래프
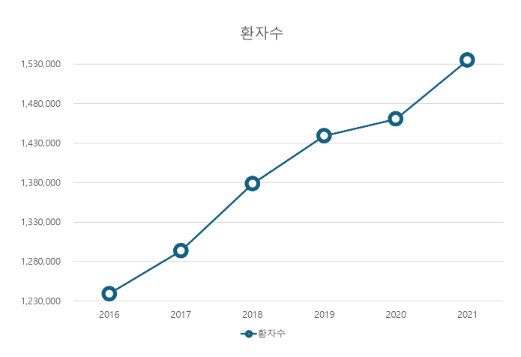
- 연속적 자료에서, 관찰 대상의 추이를 비교하거나 경향성/추세(Trend) 관찰, 예측 가능성
분포시각화 탐색
- 시간 기준이 아니며 데이터가 차지하는 영역을 기준으로, 범주형 데이터나 연속형 데이터를 구간화하여 데이터의 분포 등을 이해하는데 효과적
파이차트(Pie Chart)
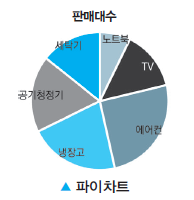
- 비율 한눈에 볼 수 있음, 백분율에 대한 상대적 차이 비교
도넛차트
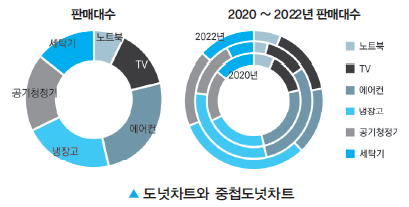
줄기잎그림(Stem & Leaf Plot)
- 관측값의 정보를 손실 및 변환 없이 그대로 분포를 파악할 수 있는 장점
- 모든 자료를 표현하기 때문에 자료가 많으면 파악 어려움
트리맵
히스토그램(Histogram)
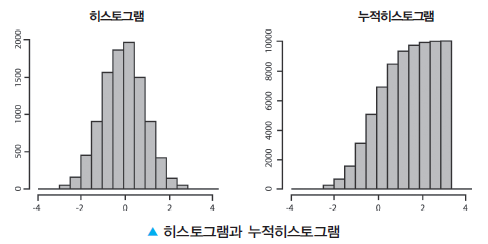
- 보통 가로축이 계급(구간), 세로축이 도수(빈도 수)
상자그림(Box Plot)
관계시각화 탐색
산점도(Scatter Plot)
- 군집화, 이상치 패턴 파악하는데 유용
- 상관관계 분석에서 두 변수 간의 선형/비선형 형태를 파악해 방향성과 강도 조사 가능
버블차트(Buuble Chart)
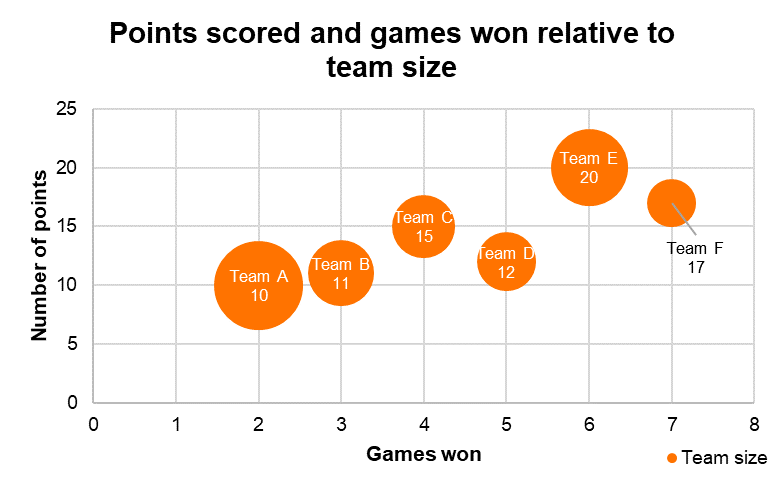
- 산점도를 확장하여 3가지 요소에 대해 상관관계를 표현할 수 있는 시각화 방법
- 버블의 크기로 비율 나타내기, 버블의 모양을 데이터의 패턴에 따라 시각화
비교시각화 탐색
- 다변량 변수를 포함하는 자료를 3차원 공간에 효과적으로 표현하는 시각화 방법
플로팅바차트(Floating Bar Chart)
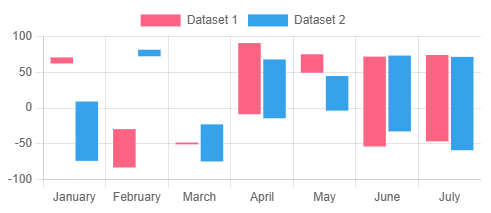
- 가장 높은 수치부터 가장 낮은 수치 범주 간 중복, 이상치 파악이 가능
평행좌표그래프(Parallel Coordinates Plot) = 병렬차트
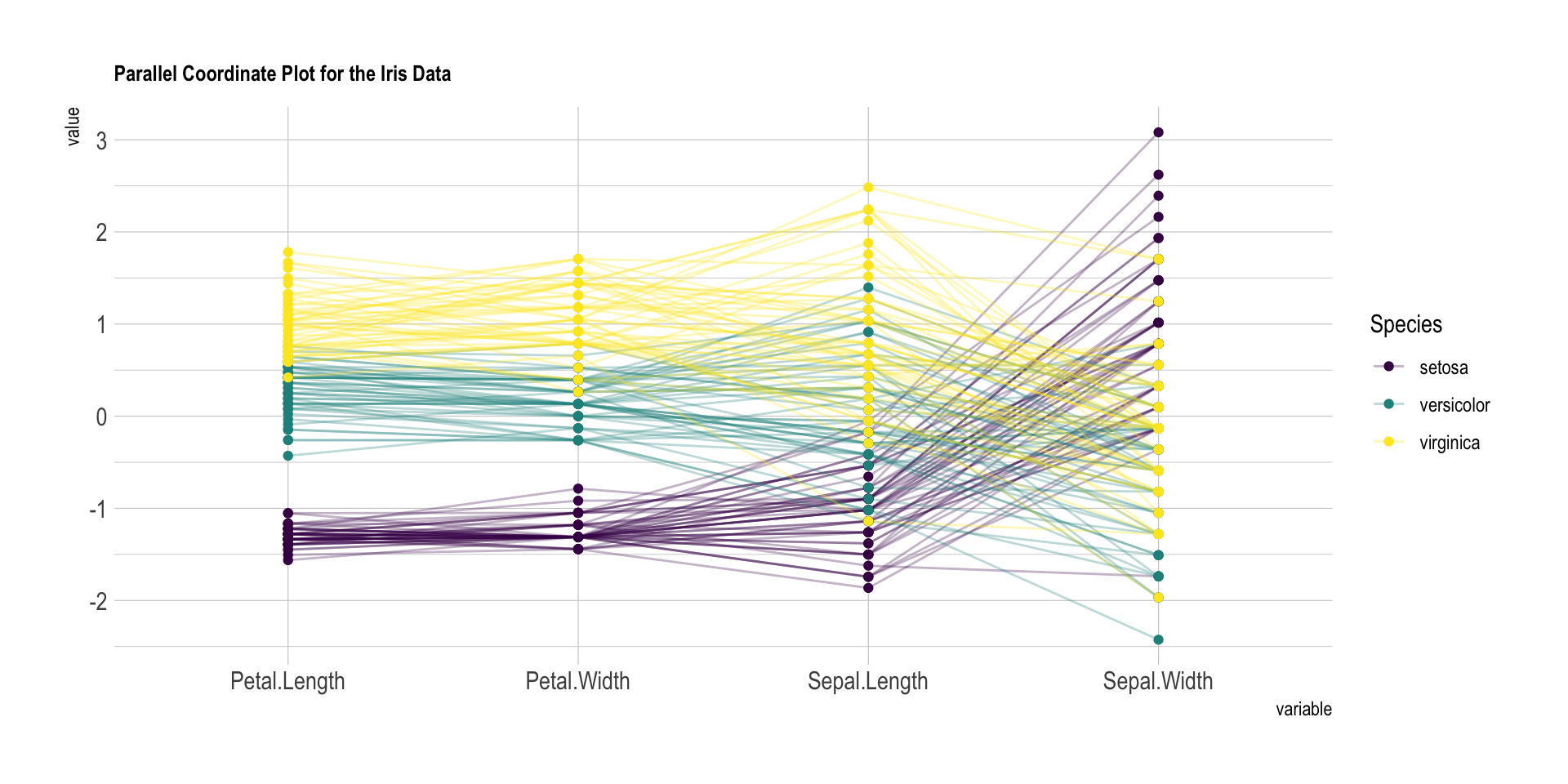
- 한 번에 많은 데이터를 비교하기에 유용
- 한 레코드(Raw Data)별로 주어진 값을 해당 변수 축에 대응시켜 선으로 연결, 레코드 수만큼의 라인
+ 붓꽃(Iris) 데이터셋
- Iriss Dataset은 통계학자 피셔(R.A Fisher)의 붓꽃 분류 연구에 기반한 데이터
- 꽃받침 길이(Sepal Length), 꽃받침폭(Sepal Width), 꽃잎 길이(Petal Length), 꽃잎 폭(Petal Width), 붓꽃 종(Species)
- 5가지 변수, 150라인
공간시각화 탐색
- 실제 위치정보를 표현한 시각화 방법
'빅데이터분석기사' 카테고리의 다른 글
| [빅데이터분석기사 필기] 고급 데이터 탐색 (1) | 2025.03.01 |
|---|---|
| [빅데이터분석기사 필기] 데이터 탐색 기초 출제예상문제 오답노트 (0) | 2025.02.28 |
| [빅데이터분석기사 필기] 분석 변수 처리 출제예상문제 오답노트 (0) | 2025.02.27 |
| [빅데이터분석기사 필기] Day8: 분석 변수 처리 (0) | 2025.02.27 |
| [빅데이터분석기사 필기] 데이터 정제 출제예상문제 오답노트 (0) | 2025.02.26 |
