지도학습 - 회귀모델의 평가지표
SSE(Sum Squared Error)
- 실제 값과 예측 값의 차이를 제곱하여 더한 값
MSE(Mean Squared Error)
- 실제 값과 예측 값의 차이의 제곱에 대한 평균을 취한 값
RSME(Root Mean Squared Error)
- MSE에 루트를 취한 값, 평균제곱근 오차
결정계수 R^2
- 회귀모형이 실제 값에 대해서 얼마나 잘 적합하는지에 대한 비율
비지도학습 - 군집분석의 평가지표
실루엣 계수
Dunn Index
오차행렬(혼돈행렬, Confusion Matrix)
- 머신러닝 중 분류(Classification) 모델의 정확도를 2x2 행렬로 나타내는 방법
- 알고리즘이 실제(actual) 값과 비교했을 때 얼마나 정확하게 값을 예측했는지는 보기 용이하게 행렬로

- True Positive (TP): 실제로 Positive인 경우를 Positive로 예측한 경우 \
- False Positive (FP): 실제로 Negative인 경우를 Positive로 예측한 경우
- False Negative (FN): 실제로 Positive인 경우를 Negative로 예측한 경우
- True Negative (TN): 실제로 Negative인 경우를 Negative로 예측한 경우
분류 모델의 평가 지표
1. 정확도(accuracy)

- 실제적인 데이터와 예측된 데이터를 비교해 동일한지 판단하는 것
- 전체 예측에서 참 긍정(TP)와 참 부정(TN)이 차지하는 비율
2. 정밀도(precision)

- Positive로 예측한 대상 중에 실제와 예측 값이 일치하는 비율
- '긍정'으로 예측한 비율 중 실제로 '긍정'(TP)인 비율
3. 재현율(=민감도; recall, sensitivity)

- 실제 Positive인 대상 중에 실제와 예측 값이 일치하는 비율
- 참 긍정률(TP Rate), Hit Ratio라고도 함
4. F1 Score

- 정밀도와 재현율의 조화 평균으로, 정밀도와 재현율의 균형을 고려한 지표
5. 오차비율(Error Rate)

- 실제 분류 범주를 잘못 분류한 비율
6. 특이도(Specificity)

- 실제 '부정'인 범주 중 '부정'으로 올바르게 예측(TN)한 비율
- 재현율의 부정ver
7. 거짓 긍정률(FP Rate)

- 실제 '부정'인 범주 중 '긍정'으로 잘못 예측(FP)한 비율
+ AUC-ROC Curve
- 분류 모델에서 예측의 성능을 평가하는 지표
- 다양한 임계값에서 모델의 성능을 시각적으로 평가
- AUC는 이 곡선 아래 면적을 의미하며, 1에 가까울수록 성능이 좋음
정규성 검정의 종류
1. Kolmogorove - Smirnov Test: 표본의 수(n)가 2,000개 초과인 데이터셋에 적합
2. Shapiro-Wilks Test: 표본의 수(n)가 2,000개 미만인 데이터셋에 적합
3. Quantile - Quantile Plot: 정규분포 판단하는 시각적인 분석방법, 표본의 수(n)이 소규모일 때 적합
잔차 진단
- 회귀분석에 독립변수 및 종속변수의 관계를 규정하게 되는 최적의 최귀선은 잔차(실측치 예측치 차이)를 가장 작게 해주는 선
- 잔차의 합=0, 잔차는 추세나 패턴이 없음
1. 잔차의 독립성 진단
- 패턴이 없음, Durbin-Watson 검정
2. 잔차의 정규성 진단
- 정규분포 및 잔차의 분포 비교, Q-Q Plot
3. 잔차의 등분산성 진단
- 잔차의 분산이 특정한 패턴이 없이 순서와는 무관하게 일정
교차검증
- 과적합 예방, 오랜 시간이 걸릴 수 있음, 일반화 능력 테스트
- k-fold 교차검증 기법: 전체 데이터셋을 k개의 서브셋으로 구분해 k번의 평가를 실행, 중복없이 병행진행 후 평균=성능
1. k-fold 교차검증(k-fold cross validation)
- 가장 통상적, 과적합 방지 + 모든 데이터 활
- 문제점: 불균형한 데이터에 적용 안 됨
- 일반화 성능을 만족시키는 최적의 하이퍼 파라미터를 구하기 위한 모델 튜닝에 사용
학습 및 검증 반복
a. 각 fold가 한 번씩 검증 데이터로 사용
b. 나머지 k-1개의 fold는 훈련 데이터로 사용
c. 이렇게 k번 반복하여 각각의 fold가 한번씩 검증 데이터로 사용
홀드아웃 기법(holdout method)
- 초기의 데이터셋을 별도의 훈련 세트와 테스트 세트로 구분
- 전통적이면서 널리 사용되는 머신러닝 모델의 성능 추정 방법
- train_test_split
리브-p-아웃 교차검증(leave-p-out cross validation)
- 전체 데이터(서로 다른 데이터 샘플들) 중에서 p개의 샘플을 선택해 모델 검증에 확용
- k-fold는 데이터셋 중 1/k를 검증으로 한다면, 이건 p/전체 데이터셋을 검증에 사
- p=1이면 리브-원-아웃 교차검증(LOO CV)
계층별 k-겹 교차검증(stratifieed k-fold cross validation)
- 주로 분류(classification) 문제에서 활용, label의 분포가 각 클래스별로 불균형할 때
- 인덱스 순으로 데이터 폴드 세트 구성 X(치명적 오류 발생 가능), label의 분포 고려
모수 유의성 검정
1. 모집단 및 모수의 관계

2. 가설검정의 유형

| Z-검정 | t-검정 |
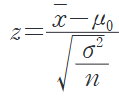 |
 |
ANOVA(Analysis of Variance)
| 종류 | 내용 |
| 일원분산분석 | - 하나의 독립변수에 따른 집단 간 차이 - 하나의 독립변수의 변화가 종속변수에 미치는 영향 분석 |
| 이원분산분석 | - 2개의 독립변수에 따른 집단 간 차이를 비교 - 하나의 독립변수의 변화가 독립변수에 미치는 영향이 타 독립변수의 수준에 의해 달라지는지 분석 |
적합도 검정(Goodness-of-fit 검정)
- 데이터의 분포가 특정한 분포함수와 얼마나 맞는지 검정
- 적합도 검정은 관측도수와 기대도수 차이에 기초를 두고 카이제곱 값 검정통계량을 사용
- 모든 기대도수가 5보다 큰 경우에만 적용 가능, 카테고리수-1의 자유도를 갖는 카이제곱분포를 따름
1. 카이제곱 검정(Chi-Squared Test)
- 범주형 데이터의 분포가 기대 분포와 일치하는지를 검정하는 방법
- 기대 빈도와 실제 빈도의 차이를 기반으로 검정
- 표본 크기가 클 때 유용함
2. 콜모고로프-스미르노프 검정(K-S Test)
- 연속형 데이터의 분포가 특정 분포(정규분포 등)를 따르는지 검정
- 누적분포함수(CDF)의 최대 차이를 이용하여 비교
- 정규성 검정뿐만 아니라 두 분포 비교에도 사용됨
3. 샤피로-윌크 검정(Shapiro-Wilk Test)
- 데이터가 정규분포를 따르는지 검정하는 방법
- 작은 샘플에서도 효과적이며, 정규성 검정에 자주 사용됨
- p-value가 작으면 정규성이 있다고 보기 어려움.
4. Q-Q 플롯
- 그래프를 활용해 정규성의 가정을 시각적으로 검ㅁ정
- 대각선의 참조선을 따라 값들이 분포하면 정규성 만족
- 그래프에 대한 해석이 주관적이므로 보조적 활용
- 한 쪽으로 치우치는 모습일 경우 정규성 가정에 위배되었다고 볼 수 있음
5. 비모수적 검정
- 모집단에 대한 정보가 없거나 특정한 확률분포를 따른다고 전제할 수 없을 때
- 실제 값보다는 부호나 순위 등의 형태를 이용하는 경우가 많음
| 표본 | 검정방법 | ||
| 서열척도 | 명목척도 | ||
| 단일표본 | Kolmogorov-Smirnov 검정 | 카이제곱검정 Run 검정 |
|
| 종속표본 | 2개 | 부호 검정 윌콕슨(Wilcoxon)의 부호 순위검정 |
Mcnemar 검정 |
| k개 | Friedman 검정 | Cochran의 Q검정 | |
| 독립표본 | 2개 | Wilcoxon의 순위합 검정 Mann-Whitney U 검정 Kolmogorov-Smirnov 검정 Moses의 극단반응 검정 |
카이제곱 검정 Fisher의 정확확률 검정 |
| k개 | 중위수 검정 Kruskai-Wallis 검정 |
카이제곱검정 | |
'빅데이터분석기사' 카테고리의 다른 글
| [빅데이터분석기사 필기] 분석결과 해석 (1) | 2025.03.10 |
|---|---|
| [빅데이터분석기사 필기] 분석 모형 개선 (0) | 2025.03.09 |
| [빅데이터분석기사 필기] 분석 기법 적용 (0) | 2025.03.07 |
| [빅데이터분석기사 필기] 분석 절차 수립 (0) | 2025.03.06 |
| [빅데이터분석기사 필기] 추론통계 출제예상문제 오답노트 (1) | 2025.03.05 |