확률의 계산
복원추출과 비복원추출
- 복원추출(Sampling with Replacement): 추출된 원소를 다음 표본추출 대상에 포함, 중복 가능, 독립사건
- 비복원추출(Sampling without Replacement): 추출된 원소 제외, 표본공간이 바뀌어 종속사건
복원추출과 비복원추출 확률 계산
| 구분 | 설명 | |
| 예시 | 네모박스에 공이 10개가 있고, 검은색 공 7개와 빨간색 공 3개가 들어 있다고 하자. 연속해서 2개의 공을 뽑았을 때 빨간색 공을 뽑을 확률은 아래와 같다. | |
| 비복원추출 (종속사건) |
첫 번째 공 선택이 빨간색 공일 확률 | P(A) |
| 두 번째 공 선택이 빨간색 공일 확률 | P(B) | |
| 첫 번째 공과 두 번째 공이 빨간색 공일 확률 | P(A ∩ B) = P(A) × P(B|A) 3 / 10 × 2 / 9 = 6 / 90 = 1 / 15 |
|
| 복원추출 (독립사건) |
첫 번째 공 선택이 빨간색 공일 확률 | P(A) = 3 / 10 |
| 두 번째 공 선택이 빨간색 공일 확률 | P(B) = 3 /10 | |
| 첫 번째 공과 두 번째 공이 빨간색 공일 확률 | P(A ∩ B) = P(A) × P(B) 3 / 10 × 3 / 10 = 9 / 100 |
|
경우의 수(The number of case)
- 어떤 실험을 했을 때 발생할 수 있는 결과의 개수, 즉 원소의 개수
곱의 법칙 사례
| 구분 | 설명 |
| 사례 | 동전 3개를 던져서 뒷면이 2번 나오는 경우의 수 |
| 각 실험 집합 | 동전1 = {앞, 뒤}, 동전2 = {앞, 뒤}, 동전3 = {앞, 뒤} |
| 가능한 실험의 결과 | 동전1 = 2, 동전2 = 2, 동전3 = 2 |
| 3번 실험한 결과의 집합 | 2 x 2 x 2 = 8 |
| 동전 뒷면이 2회 나오는 경우의 수 | 3 |
| 동전 3개를 던져 뒷면이 2번 나오는 확률 | 3 / 8 |
순열과 조합 요약
| 배열/추출 | 복원(중복허용) | 비복원(중복허용 안 함) |
| 순서 고려 | 중복순열 순서를 고려하면서 복원추출 |
순열 순서를 고려하면서 비복원추출 |
| 순서 무시 | 중복조합 순서를 고려하지 않고 복원추출 |
조합 순서를 고려하지 않고 비복원추출 |
확률변수와 확률분포의 이해
확률변수(Random Variable): 확률 실험의 결과를 수치로 나타낸 변수
확률함수(Probability Function): 확률변수에 의해 정의된 실수를 0과 1사이의 확률로 대응시키는 함수
확률분포(Probability Distribution): 확률변수가 특정한 값을 가질 확률을 나타내는 함수 또는 표
이산확률변수와 이산확률분포

- 이산확률변수: 확률변수 X가 셀 수 있는 특정한 수치(정수)만을 가질 때 ex. 불량품 수, 고속도로 사고 건수, 방문자 수
- 이산확률분포: 이산확률변수의 값 각각에 대한 화률의 대응관계
- 확률질량함수(PMF: Probability Mass Function): 이산확률변수의 확률질량함수

- 이산누적분포함수(CDF: Cumnulative Distribution Function): 이산확률변수 X가 xi이상 xj이하의 값을 가질 확률
확률분포표
| 확률변수 X | x1 | x2 | ... | xn |
| 확률질량함수 P(X = xi) | p1 | p2 | ... | pn |
연속확률변수와 연속확률분포

- 연속확률변수: X가 어떤 범위(구간)에서 연속적인 값(실수)을 취할 수 있는 확률변수
- 연속확률함수: X가 어떤 값 x를 가진 확률
- 확률밀도함수(PDF: Probability Density Function): 확률함수 f(x) = P(X = x)
확률변수의 기대값과 분산
확률변수의 기대값: 각 확률변수가 특정 값을 가질 확률들을 곱하여 합한(더한) 값, 평균 또는 중심위치
확률변수의 분산: 확률변수 X의 특정 x가 발생할 확률에서 기대값을 뺀 값(편차)의 제곱
이산확률변수의 기대값과 분산
이산확률변수 X와 임의의 상수 a, b(a≠0)에 대하여 아래의 규칙이 성립된다.
- 평균: E(aX+b)=aE(X)+b
- 분산: V(aX+b)=a^2V(X)
- 표준편차: SD(aX+b)=|a|SD(X)
연속확률변수의 기대값과 분산
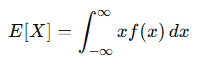
- 기대값(Expected Value)
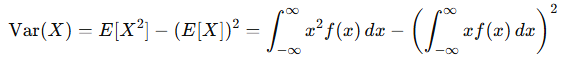
- 분산(Variance)
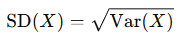
- 표준편차(Standard Deviation)
이산확률분포의 종류
- 이산형균등분포
- 베르누이분포
- 이항분포
- 초기하분포
- 기하분포
- 음이항분포
- 포아송분포
1. 이산균등분포(Discrete Uniform Distribution)
- 확률변수 X가 n개의 이산값 {x1, x2, x3, ... , xn}을 가지며 각 값들이 취할 확률이 동일한 경우
- 예) 주사위 1회 던지는 확률 실험: 주사위 수가 나올 확률은 각각 1/6로 같음
2. 베르누이분포(Bernoulli Distribution)
- 베르누이 시행(Bernoulli Trial): 확률 실험의 결과가 성공(Success, S) 혹은 실패(Failure, F)로만 나오는 실험
- 예) 한 개의 동전을 던지면 앞면 또는 뒷면의 오직 두 가지 결과로 나누고, 앞면이면 1 뒷면이면 0을 갖는 확률변수 X
3. 이항분포(Binominal Distribution)
- '성공'에 해당하는 사건이 바출현할 확률이 p인 똑같은 베르누이 시행을 독립적으로 n번 시행하여 일어난 두 가지 결과에 의해 그 값이 0과 1로 결정되는 확률분포
- 예) 축구선수가 패널티킥을 찬다고 했을 때, 60%의 성공확률로 10번 시행 8번 성공 확률: 10C7·(0.6)^8(0.4)^2
4. 초기하분포(Hypergeometric Distribution)
- 초기하분포는 비복원추출로 매 시험조건이 달라지며, 모집단 N이 충분히 크면 이항분포를 따른다. (이항분포는 독립시행, 복원추출로 실험 조건이 일정)
- 예) 불량품이 6개 포함된 10개의 제품으로부터 7개를 비복원(임의로) 추출하여 조사할 때, 불량품이 4개 나올 확률실험
5. 기하분포(Geometric Distribution)
- 베르누이 시행을 독립적으로 반복해 나가는 시행에서 확률변수 X를 첫 번째 성공이 발생할 때까지 총 시행횟수라고 정의하면, 이 확률변수는 기하분포를 따른다.
- 예) 연애를 해서 결혼할 확률이 10%라 가정했을 때, 확률변수 X는 x번째 사귄 사람과 결혼할 확률
+무기억성
- 기억성(Memory Property): 과거, 현재, 미래가 상호 의존적인 특성
- 무기억성(Memoryless Property): 과거의 사건이 미래 정보와 전혀 관련성을 갖고 있지 않는 특성. 연속확률분포의 지수분포 또한 무기억성을 따른다.
6. 음이항분포(Negative Binomial Distribution)
- 베르누이 시행을 독립적으로 반복해 나가는 시행에서 확률변수 X를 r번째 성공이 발생할 때까지 총 시행횟수라고 정의하면 이 확률변수는 음이항분포를 따른다.
- k번의 실험에서 r번의 성공을 하기 위해선 k-1번 실험에서 r-1번 성공을 해야함
- 예) 야구선수가 안타를 칠 확률이 25%라고 했을 떄, 확률변수 X는 이 선수가 7번째 타석에서 3번째 안타를 칠 확률
7. 포아송분포(Poisson Distribution)
- 일정 시간이나 공간에서 특정 사건이 발생하는 횟수를 확률적으로 모델링하는 분포
- 독립성, 비례성, 비집락성 만족 실험
- 예) 콜센터에 1시간당 평균 5건의 전화가 걸려올 때, 특정 시간에 전화가 걸려올 확률
+ 포아송가정
- 독립성: 서로 다른 구간에서 발생하는 사건의 수는 서로 독립이다.
- 비례성: 충분히 짧은 구간에서 사건이 발생할 확률은 구간의 길이에 비례한다.
- 비집락성 충분히 짧은 구간에서 2회 이상의 사건이 발생할 확률은 거의 없다.
연속확률분포의 종류
- 연속형균등분포
- 지수분포
- 카이제곱분포(x^2분포)
- t분포
- 정규(Z)분포
- F분포
1. 연속균일분포(Continuous Uniform Distribution, 균등분포)
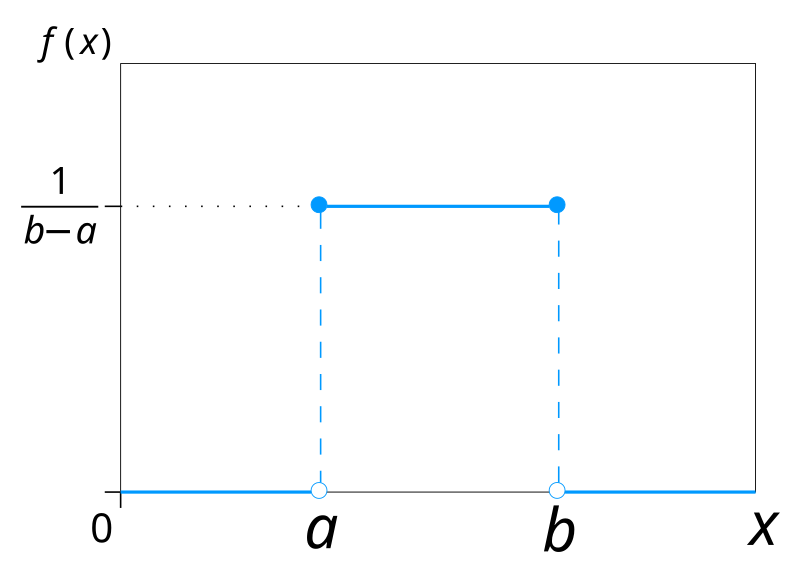
- 임의의 실수구간 a, b에서 나타날 가능성이 동일한 확률변수
- 예) 버스가 10분 간격으로 온다고 가정하면, 특정 시각에 도착할 확률이 동일함
2. 정규분포(Normal Distribution)
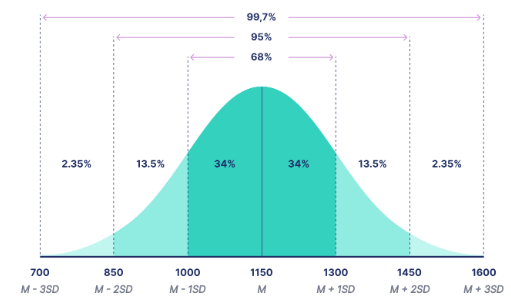
- 평균을 중심으로 좌우대칭이고 종 모양, 왜도=0, 첨도=3
3. 표준정규분포(Standard Normal Distribution)
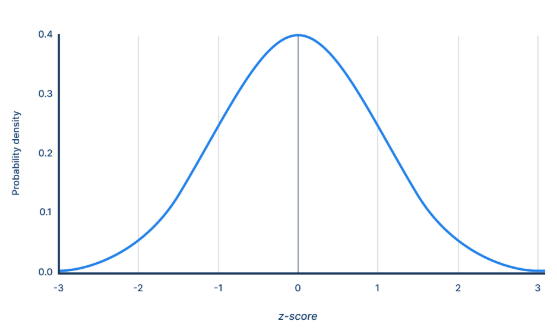
- 표준화확률변수(Standardized Random Variable) Z에 의해 변환 과정을 거쳐 평귱=0, 표준편차=1 정규분포
- Z = (X - μ) / σ
4. 감마분포(Gamma Distribution)
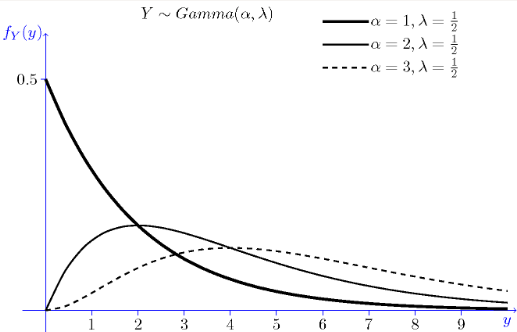
- 포아송 가정을 만족하는 실험에서, 양의 실수구간에서 정의한 어떤 사건이 α번 발생하기까지의 대기시간
- 예) 콜센터에서 3번째 전화가 걸려올 때까지 걸리는 시간, 기계 부품이 5번 고장 날 때까지의 총 가동 시간
5. 지수분포(Exponential Distribution)
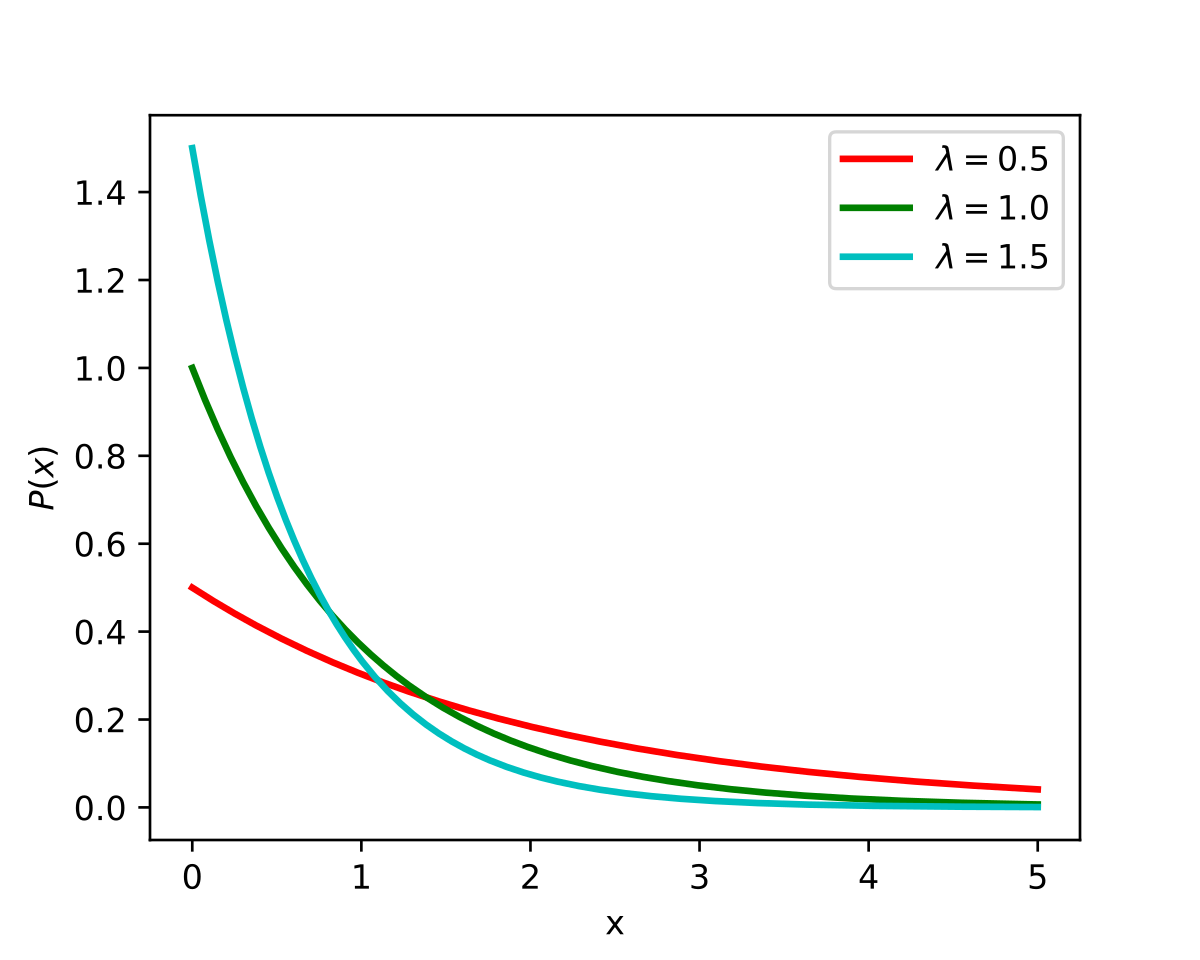
- 어떤 사건이 발생할 떄까지의 대기 시간을 모델링하는 분포. 감마분포에서 k=1일 때 지수붙포가 된다.
- 예) 콜센터에서 다음 전화가 걸려오기까지 걸리는 시간
6. 카이제곱분포(Chi-square Distribution, x^2분포)
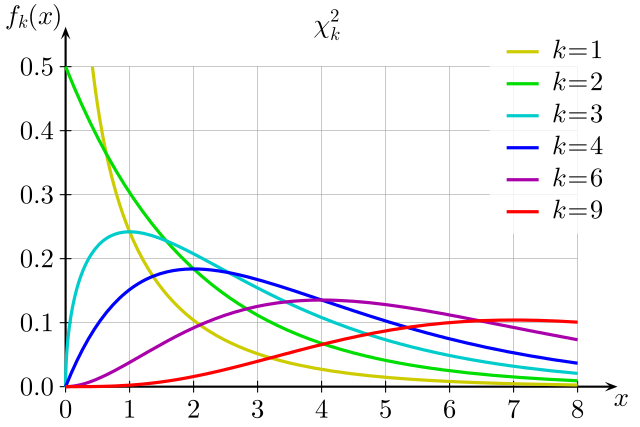
- 정규분포를 따르는 독립적인 변수들의 제곱합
+카이제곱통계량
- 카이제곱통계량은 범주형 변수인 명목척도나 서열척도 자료의 독립성 검정, 적합성 검정, 동질성 검정에 주로 활용되며, 두 변수 간 연관성 검정을 위해 사용되는 분석 기법인 교차분석의 통계량으로 사용한다.
+검정 예시
- 적합성 검정(Goodness-of-Fit Test): 기대 빈도와 실제 빈도의 차이를 검정하는 데 사용됨
- 독립성 검정(Independence Test): 성별과 제품 선호도가 독립적인지 분석할 때 카이제곱 검정을 사용함.
- 분산의 차이 검정(Variance Test): 특정 실험 그룹과 전체 모집단의 분산이 같은지 검정할 때 사용됨
정규분포와 카이제곱분포
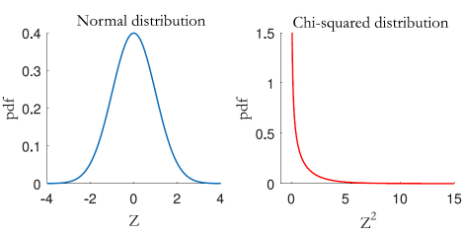
- 카이(X)는 X의 그리스 알파벳 버전으로 평균0, 분산1인 표준정규분포를 의미하기 때문에 카이제곱 >= 0인 것, 음의 값 없음
'빅데이터분석기사' 카테고리의 다른 글
| [빅데이터분석기사 필기] 기술통계 출제예상문제 오답노트 (0) | 2025.03.04 |
|---|---|
| [빅데이터분석기사 필기] 기술통계(3) (0) | 2025.03.04 |
| [빅데이터분석기사 필기] 기술통계(1) (0) | 2025.03.02 |
| [빅데이터분석기사 필기] 고급 데이터 탐색 출제예상문제 오답노트 (0) | 2025.03.01 |
| [빅데이터분석기사 필기] 고급 데이터 탐색 (1) | 2025.03.01 |